نشهد العصر الرقمي بكل إنجازاته وثورة معلوماته، هذه المعلومات تكتب وتخزن وتنقل بشكل رقمي مشفّر أو مرمّز، وقد أذهل العلماء وجود التّشفير والترميز في كل أركان الكون، بدءاً من أشكال تواصل المخلوقات إلى أنوية ذراتها، ومن أحماض الإنسان وصفاته، إلى مائه وسيالات أعصابه. يقول خبراء نظرية المعلومات أن المعلومات إحدى الخصائص الأساسية للكون، شأنها شأن المادة والطاقة، وكما أن الكتلة هو التعبير عن المادة، فإن التنظيم هو التعبير عن المعلومات، والتّشفير والترميز هو الحافظ لها شكلاً ومضموناً، وهو الأمان لها.

1- نظام الترميز  Coding system

إن نظام التّرميز هو ذلك الابتكار الذي سمح بالقفزة الحاسوبية التي اعتبرت مولد الحاسب الحالي، وفكرته تتلخص في الاستناد إلى الإشارات التي يتم تلقيها من أجهزة الإدخال، بحيث أنه يتم تجميع هذه الإشارات في مجموعات ذات طول محدد، ويتم فهم كل مجموعة وفقا لتعريف مسبق.

تمثيل المعلومات في الأنظمة الرقمية  Data Representation in Information Systems

حتى يتمكن أي نظام رقمي مثل الحاسب من التعامل مع أي نوع من أنواع البيانات، فإن تلك البيانات يجب أن تكون ممثلة في الشكل الثنائي (Binary)، أي في شكل مجموعة من الأصفار 0″s والواحدات 1″s، حيث يتم تمثيل القيمة المنطقية 0 بمستوى جهد معين داخل الدوائر الإلكترونية للنظام الرقمي، ويتم تمثيل القيمة المنطقية 1 بمستوى جهد آخر. مثلاً تمثل القيمة المنطقية 1 بالجهد+5 Volt  ، والقيمة المنطقية 0 بالجهد 0 Volt .

إن الأنظمة الرقمية كالحاسب وأنظمة الاتصالات لا تفقه شيئاً سوى مفهومين بسيطين هما الوجود والعدم أو الواحد 1 والصفر 0، وهكذا، فللتعبير عن أي شيء ينبغي تحويله إلى سلسلة طويلة (مجموعة) من الخانات الممغنطة وغير الممغنطة، وحسب تسلسل مغنطتها يمكن معرفة المقصود من السلسلة المحددة.

لفهم آلية استخدام نظام التّرميز نعرض مثلا من الحواسيب الحالية التي تعتمد طول المجموعة مؤلفا من ثماني إشارات، والإشارات هي شحنات كهربائية متساوية الكمية وكل منها يعبر عن إحدى حالتين، إحداهما حالة وجود شحنة والثانية حالة عدم وجود شحنة، وبالتالي فالمجموعة التي تتألف من ثماني إشارات يمكن تركيبها بعدد من الطرق مساو للعدد اثنين مضروبا بنفسه ثماني مرات، لأن كل موقع يحتمل حالتين: الوجود وعدم الوجود، أي:

2×2×2×2×2×2×2×2=256

والآن نصطلح لكل مجموعة من هذه المجموعات رمزا معينا ليعبر عنها فنحصل على نظام التّرميز.

علم التّرميز والتّعمية واستخراج المعمى Cryptography

التّعمية أو الترميز هو علم رياضي يهدف لتحويل مجموعة من المعلومات الرمزية بهدف إخفاء محتواها، إلى مجموعة أخرى مبهمة باستخدام طريقة محددة، يمكن بمعرفتها العودة إلى النص الأساسي الواضح وهو ما يسمى باستخراج المعمى.

عُرف علم التّعمية منذ القدم، إذ استخدم لإخفاء معلومات الرسائل، وانتهجت طرق ونظم رمزية عديدة من أجل ذلك. وقد يغيب عن الكثيرين أن أصله عربي وأن العرب هم آباؤه ويدين لهم ولادة ونشأة وتطوراً، ويعد كتاب الكندي «رسالة في استخراج الأعداد المضمرة»، أول مرجع معروف في علم التّعمية واستخراج المعمى واصطلح على تسميته حديثا علم الشِفرة.

يحظى علم التّعمية واستخراج المعمى بمكانة مرموقة بين العلوم، وقد أكتسب أهمية بالغة لتنوع تطبيقاته وخصوصاً في المجالات الأمنية والعسكرية والمصرفية، إذ يعتبر لغة عملٍ للتطبيقات التقنية، وأحد الأساسيات في عملها وأسلوباً لأمن معلوماتها، وله مؤسسات توفر له أسباب الرعاية والتطوير والاختبار، وتنتج أنظمة تشفير تعتمد خوارزميات معقدة وموثوقة.

القواعد الرئيسية عند القيام بعملية التّرميز The Basic  Rules  For Coding

إن أهم أسس عملية التّرميز، هو اعتماد قواعد ثابتة وخوارزميات معروفة، والإيجاز والاختصار لتقليل احتمال الأخطاء في عمليتي النقل وفك التّرميز، بالإضافة إلى استخدام رموز تكون:

• ثابتة البنية محددة الطول.
• واضحة غير متشابهة.
• قابلة للتصنيف والقراءة.
• قابلة للاسترجاع والمعالجة.
• متناغمة منطقيًا مع النظام الكلي.
• تغطي جميع الرموز المطلوبة لتبادل المعلومات.

أهداف التّرميز Coding objectives

• السرية أو الخصوصية: للحفاظ على محتوى المعلومات.
• تكامل البيانات: للحفاظ على المعلومات من التغيير (حذف أو إضافة أو تعديل).
• إثبات الهوية: إثبات هوية التعامل مع البيانات.
• عدم الإنكار: منع الشخص من إنكاره القيام بعمل ما.
• سهولة الاستخدام: بتسهيل التعامل مع المعلومات كتقليل حجمها مثلاً.

2- التمثيل الرقمي للبيانات Digital Data Representation

نظام الترميز الثّنائي Binary Code System

يعدّ نظام الترميز الثّنائي  (Binary Code System) أبسط نظم الترميز (نفسه نظام العد الثّنائي Binary Number System)، أساسه الرّقم(2) ، إذ يتكوّن من الرّمزين (1،0)، وهما إسقاط مباشر لمفهومي “العدم”  و  “الوجود”  فالعدم يعبر عنه بالعنصر “صفر” ، والوجود يعبر عنه بالعنصر “واحد “.

باستخدام رموز النظام الثنائي (1،0) يمكن تمثيل أي عدد من أي نظام عددي، إذ يتكرّران على شكل سلسلة بما يتناسب مع العدد المطلوب، ويمكن تطبيق قواعد الجبر البولياني على هذا النظام بشكلٍ مباشر، وبالتّالي تنفيذ كافة العمليات المنطقية اللازمة من أجل تكوين الدوائر الرقمية.

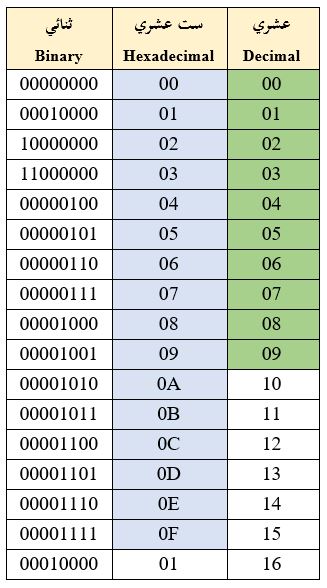
يمكن التعبير عن أي عدد بواسطة عدد ثنائي، لكن الأرقام الثنائية صعبة للفهم على الإنسان لكي يتعامل معها، لأنها تتطلب العديد من الأرقام أو الخانات في العدد الواحد، بدلاً من ذلك، غالباً ما يتم تمثيل الأرقام الثنائية في شكل أكثر قابلية للقراءة من قبل البشر، ويستخدم لذلك النظام الست عشريThe hexadecimal system, or hex  الذي يستعمل 16 رقم (0، 1، 2، 3، 4، 5، 6، 7، 8، 9، A، B، C، D، E، F) لتمثيل الأعداد الثنائية.

ويمثل كل رقم ست عشري باستخدام أربعة أرقام ثنائية، ويستخدم رقمين ست عشريين مع بعض لتمثيل  1 بايت (8 أرقام ثنائية). انظر الجدول (1-10) الذي يعرض الأرقام العشرية من 1 حتى 16 مع المكافئ لها في النظام الثنائي، والست عشري (وقد ظللنا عمود الأرقام القاعدية للأنظمة العددية).

يمكن أن تشاهد الأرقام الست عشرية، عند اختيار اللون في تطبيقات تصميم الموقع أو التطبيقات الرسومية، أو عند إدخال كلمة المرور للوصول إلى شبكة لاسلكية.

ولدينا النظام العشري decimal system  الذي نعرفه يتألف من عشرة أرقام  (0، 1،2، 3، 4، 5، 6، 7، 8، 9). النظام الثنائي binary system يتكون من رقمين فقط صفر 0 وواحد 1. وتعتمد لغة وشفرة عمل الحاسب الثنائية (المثاني) على نظام العد الثّنائي.

لغة عمل الحاسب الثنائية Binary Computer Working Language

تكتب البرامج الحاسوبية على شكل تعليمات وتراكيب حسابية ومنطقية بإحدى لغات البرمجة، إذ تجري ترجمة هذه التعليمات والتراكيب إلى سلاسل من الرموز الرقمية الثنائيّة أصفار وواحدت (0،1) التي تعبّر عن شيفرة يفهمها الحاسب تدعى لغة الآلة Machine Language.

تعتمد لغة وشفرة عمل الحاسب الثنائية (الآلة) نظام العد الثّنائي، إذ تستخدمها الأجهزة والأنظمة الرّقميّة كالحواسيب وأنظمة الاتّصالات في الدّوائر الإلكترونيّة الرّقميّة (Digital Electronic Circuits)، إذ أن هذه الدوائر عند معالجة البيانات، وتخزينها، ونقلها، وحتى إرسالها، لا تستطيع أن تفهم إلا البيانات الثنائية، أي البيانات التي تكون على شكل سلاسل من الأصفار والواحدات.

تعد الشفرة الثنائية أساس الثورة الرقمية بالكامل، وتأتي أهميتها من كونها نظام التشفير (الترميز) المستخدم لتمثيل المعلومات والبيانات ضمن الحواسيب والأنظمة الرقمية، إذ يعدّ من أبسط أنواع أنظمة التّشفير، فالعلوم والمعلومات اليوم بأشكالها وأنواعها تُمثّل وتُكتب وتُعالج وتخُزّن وتُوثّق وتُنشر وترُسل باستخدام الرموز الرقمية الثنائيّة الأصفار والواحدات (0،1)، وذلك على شكل شِفرات (إشارات)، هذه الإشارات هي سلسلة من شحنات كهربائيّة متساوية الكميّة، الخانة الواحدة في السّلسلة تسمّى بت، ومجموعة 8 بتات تشكل البايت Byte.

” بت ” = bit أو (bit=binary digit)

Bit = 1 Byte 8

تخزّن في هذه الخانة الثنائية إحدى القيمتين، الأولى حالة وجود شحنة واحد (1)، والثانية حالة عدم وجود شحنة صفر (0)، لتشكل بيانات مصفوفة من هذه الأصفار والواحدات، تتم معالجتها ضمن الأنظمة الرقمية، ومن ثم يتم تحويل ناتج المعالجة للشكل الذي نستوعبه، ويتم إظهاره.

وقد أشار القرآن الكريم لهذه اللغة باستخدام نفس الكلمة القرآنية {المثاني} في الإشارة إلى شفرة ولغة عمل الحاسب الثنائية، شفرة المثاني، وكلمة {المثاني} تكرّرت في القرآن الكريم مثاني، وجاء ذلك في مثاني من الآيات هي:

قال الله سبحانه وتعالى في الذكر الحكيم:

﴿ وَلَقَدْ آتينَكَ سَبْعاً مّنَ الْمَثَانِي وَالْقُرْآنَ الْعَظِيمَ ﴾[الحِجر: 15/87].

﴿ اللَّهُ نزَّلَ أَحْسَنَ الْحَدِيثِ كِتَٰبًا مُّتَشَٰبِهًا مَّثَانِيَ تقْشَعِرُّ مِنْهُ جُلُودُ الَّذِينَ يَخْشَوْنَ رَبهُمْ ثُمَّ تَلِينُ جُلُودُهُمْ وَقلُوبهُمْ إِلَىٰ ذِكْرِ اللَّهِ ذَٰلِكَ هُدَى اللَّهِ يهْدِي بِهِ مَن يَشَاءُ وَمَن يُضْلِلِ اللَّهُ فَمَا لَهُ مِنْ هَادٍ ﴾[الزّمر: 39/23].

إن كلمة {المثاني} القرآنيّة هي إشارة علمية قرآنية صريحة إلى لغة وشِفرة عمل الحاسب المثاني، الأصفار والواحدات، التي تدعى أيضاً لغة عمل الآلة.

إن الإشارة القرآنيّة للغة وشِفرة نقل المعلومة الكونيّة، هو سبق قرآني وإعجاز علميّ، فهذه الشفرة هي لغة الإعجاز الجديد لكتاب الله سبحانه وتعالى بلغة القرن الواحد والعشرين، لغة نظام عمل أنظمته وتقنيّاته، لغة وأبجديّة توحيد كل تقنيّات العلم وأدواته.

البايت ومشتقاته Bytes and Multiples

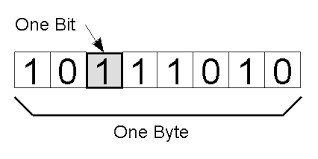
البت Bit أو الخانة الثنائية: الخانة الواحدة في السلسلة تسمى بت bit، إذن فالـ “بت” هو موقع واحد يحتمل فقط أحد خيارين: إما أن يكون مشحونا أو خاليا من الشحنة.

الخطوة التالية هي تحديد طول معياري للسلسلة بحيث كلما مضى عدد من الخانات بطول هذه السلسة المعيارية نقوم بتفسير الترميز.

البايت:Byte  هو سلسلة ذات طول ثابت من الخانات الثنائية، تتوزع الشحنات على السلسلة بشكل مختلف في كل مرة، ومقابل كل طريقة لتوزيع الشحنات يتم الاصطلاح على رمز يقابل ذلك الموضع. والطول الثابت للسلسلة يحدد حاليا بثماني خانات خصوصا بالنسبة للبنية المعتمدة في تهيئة الأجهزة المادية، الشكل (1) يظهر البايت والبت.

مضاعفات البايت، الجدول (2):

 

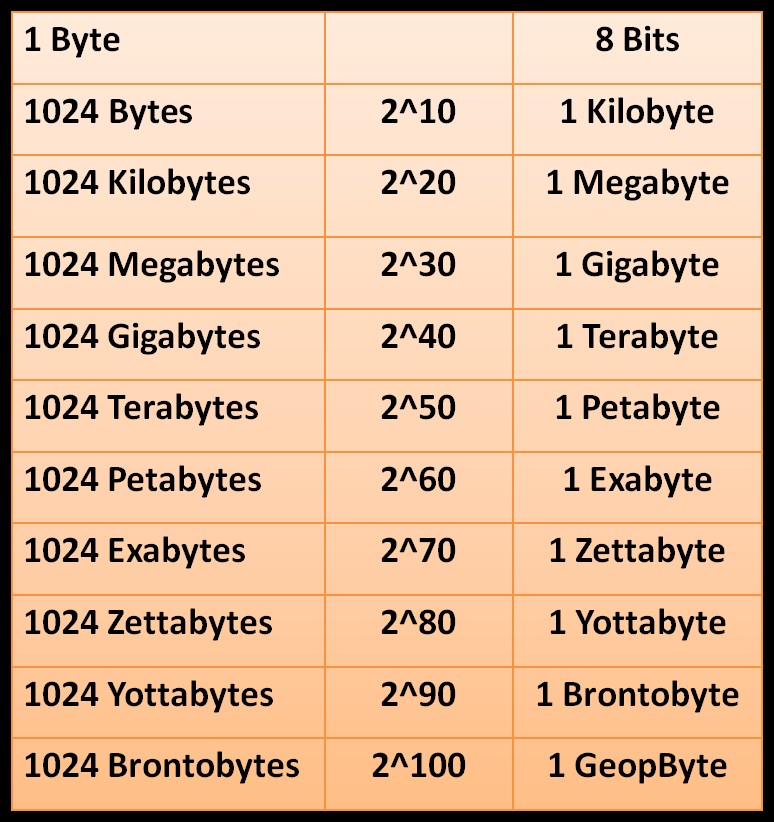
الكيلوبايت يساوي 2¹⁰= 1024 بايت.

الميغابايت تساوي 2²⁰ بايت، أو 2¹⁰كيلوبايت.

الغيغابايت تساوي 2³⁰ بايت، 2²⁰ كيلوبايت، أي 2¹⁰ميغابايت.

التيرابايت تساوي 2⁴⁰ بايت، 2³⁰ كيلوبايت، أي 2²⁰ميغابايت، أي 2¹⁰ غيغابايت.